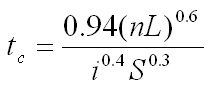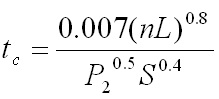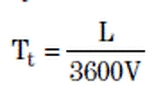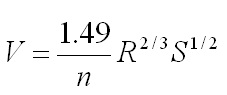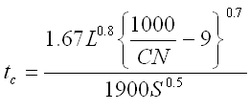Some definitions are repeated here for better understanding of the time of concentration concept. It is one of the most important concept in hydrology for accurately computing peak discharges and runoff hydrographs.
- HYDROGRAPH: Hydrograph is the graph of Flow vs. Time. The unit of flow could be cfs, m3/s, etc and the unit of time could be hours, days, months etc. The area under a hydrograph between two points (time interval) represents the volume of water passing through point of interest in that time interval. The total area under the hydrograph represents total runoff volume for that storm event.
- DIRECT RUNOFF HYDROGRAPH: Direct runoff hydrograph is the hydrograph excluding the contribution from the groundwater flow or baseflow.
- BASEFLOW It is the groundwater discharge into the streams. Baseflow is very important during dry period. It provides the very important flow to sustain the stream ecology and biology during rainfree time period.
- TIME OF CONCENTRATION: It is the time required by the entire drainage area to contribute to the runoff. If the rainfall duration is not enough for the entire drainage to contribute to the flow at a point of interest, then tc can be estimated as time from the from the start of excess rainfall to the inflection point on the recession limb.
- LAG TIME: It is the time from center of mass of excess rainfall to the center of mass of direct runoff hydrograph. Some variation in this interpretion is common, but the whole point is to interpret the position of runoff hydrograph relative to the rainfall causing the runoff. One estimate of lag time as provided by NRCS is that: tl = 0.6*tc
- SHEET FLOW: It is the flow of water over the plane surface as a more or less uniformly thick film or sheet of water.
- SHALLOW CONCENTRATED FLOW: At the end of sheet flow, water starts to accumulates into small gullies and grass swales. It is not concentrated yet to the point that it can be defined as channel (as shown as blue lines on USGS quad maps), however it clearly is not flowing as thin sheet of water flow. It is a transistion between sheet flow and channel flow.
- UNIT HYDROGRAPH: Unit Hydrograph is the hydrograph of one inch of excess rainfall distributed uniformly over the drainage area for a given rain duration 'D'(hr). This is known as D-hr Unit Hydrograph. D-hr unit hydrograph can be used to compute any other duration unit hydrograph using hydrograph lagging procedures such as S-hydrograph. In practice, however, most applications include use of SCS dimensionless unit hydrograph. Check Out SCS Dimensionless Unit Hydrograph or Delmarva Unit Hydrograph for details.
Time of Concentration
Remember that to compute the time of concentration, we are looking for a point from where it will take the longest time to travel to the drainage area outlet. This point does not necessarily have to have the longest distance to the drainage outlet.
To compute the time of concentration, several methods are
in use. The prominent is the one that uses computation of time for sheet flow,
shallow concentrated flow and open channel flow separately and add them to get
overall time of travel or time of concentration. (Also known as Velocity Method)
Sheet Flow
For sheet flow calculations, the most used equations are American Society of
Civil Engineer's (ASCE's) kinematic wave equation, U.S.Federal Highway
Administration's equation, and SCS TR-55 Manning's kinematic solution.
ASCE Kinematic wave equation:
Following is the ASCE's kinematic wave equation for calculating overland flow.
This equation is applicable for flow length's upto 300 ft.
Where,
tc = time of concentration (minutes)
i = rainfall intensity (in/hr)
L = overland flow length (ft)
n = manning's roughness coefficient
S = slope of the surface (ft/ft or m/m)
Application of this equation requires an iterative process, where you need to
pick rainfall intensity for some duration for given return period then compute
the time of concentration. You need to repeat this procedure until the chosen
duration approximately equals the computed time of concentration.
SCS TR 55 Manning's Kinematic Solution:
To avoid the iterative process, SCS TR 55 proposes the following equation for
computing sheet flow travel time:
Above equation is applicable for sheet flow lengths of upto 300 ft. Experts
recommend different allowable sheet flow lengths and varies anywhere from
100 to 300 ft. It is a good idea to check with the regulatory agency for guidance.
In the above equation,
tc = time of concentration (hr)
P2 = 2 year, 24 hour rainfall (in)
n = manning's roughness coefficient (Values published in TR 55 are shown below).
S= slope of hydraulic grade line -ft/ft or m/m-(Land slope).
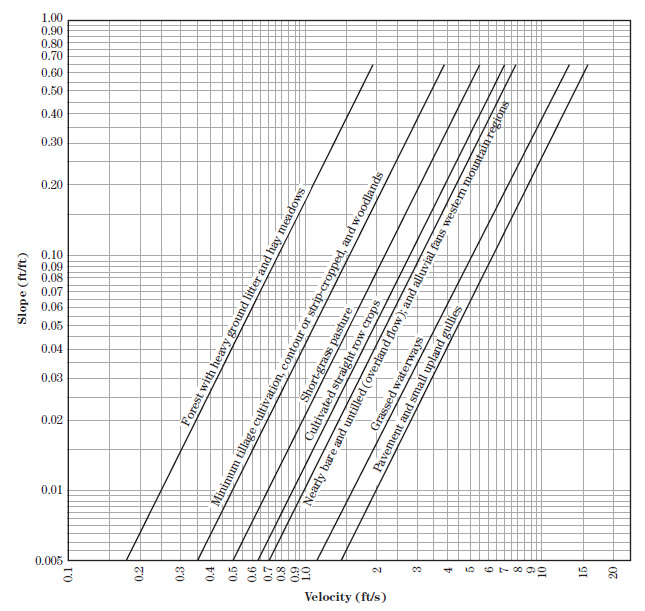
Shallow Concentrated Flow
After about 300 feet, the water flow starts to concentrate, (e.g., flow in small grass swales) and can no longer
be computed using sheet flow formulas. It is necessary to determine velocity for
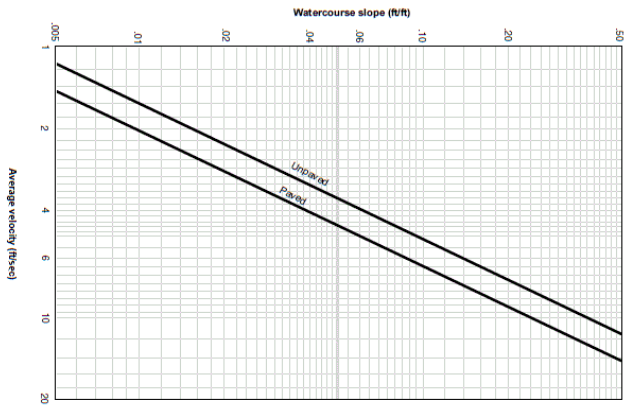
this flow and compute the time of travel. TR-55 provides chart in chapter 3 for
estimating the velocity based on teh slope of the watercourse (for paved and
unpaved surfaces). The travel time is computed by dividing the travel length
by velocity. See chart below for velocity estimates.
Here,
Tt = travel time for shallow concentrated flow (hr)
L = length of travel (ft)
V = Velocity (ft/s) - see chart below
The graph above is developed using Manning's equation for the following two
conditions:
Paved surface: Hydraulic radius = 0.2 ft, Roughness coefficient = 0.025
Velocity V = 20.328(S)0.5ft/s
Unpaved surface (Grassed waterways): Hydraulic radius = 0.4 ft,
Roughness coefficient = 0.050
Velocity V = 16.135(S)0.5ft/s
If you are trying to compute the shallow concentrated flow through different
land use than the two mentioned above, you may choose appropriate curve shown below:
Channel Flow
After shallow concentrated flow, the begins as an open channels and they generally
are visible on aerial photographs or on USGS quadrangle maps as blue line streams.
The average velocity is determined using Manning's equation and is estimated as
velocity for the bankfull stage of the channel. Manning's coefficient can be obtained
from standard texts or from government agency manuals.
Once you compute all three modes of travel, i.e., Sheet flow travel time, Shallow concentrated flow travel time and Channel flow travel time, add all three travel times, to get the time of concentration of the drainage area of interest.
As noted in the National Engineering Handbook, Folmar and Miller (2008) found that
velocity method described above tends to underestimate the time of concentration.
Following should be addressed to avoid such underestimation:
1. Consider stream sinuosity in calculating stream length
2. Consider the pools in the stream as they slows down the flow and thereby
reduces the flow velocity.
3. Don't underestimate the Manning's roughness coefficient 'n' within the
channel.
Other Formulas:
SCS Lag equation
SCS Lag equation is used to calculate time of concentration and is applicable
for watersheds under 2000 acres. It tends to overestimate the flow for mixed areas
of pervious and impervious covers.
In the above equation,
CN = SCS runoff curve number
S = average watershed slope (%)
L = hydraulic length of the watershed - longest flow path, ft