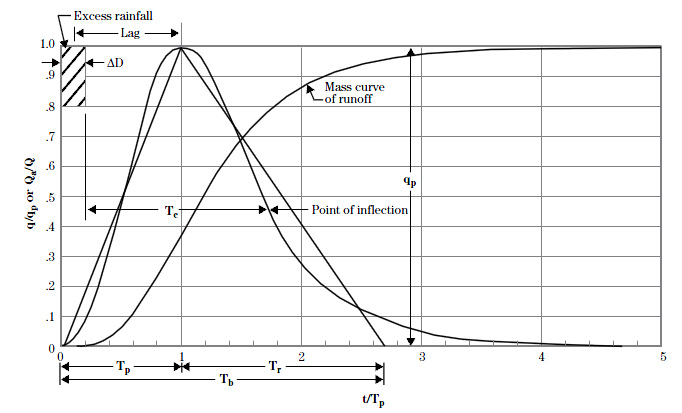
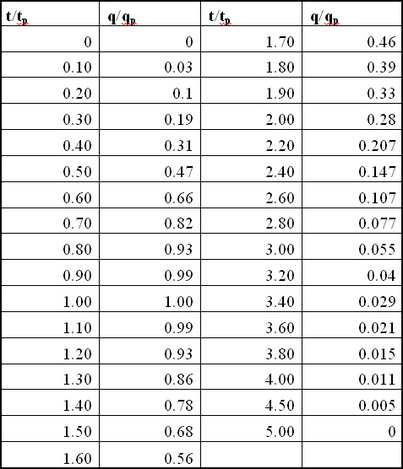
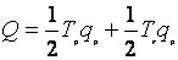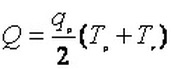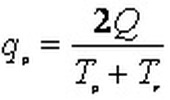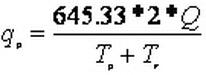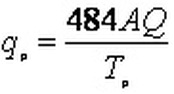Soil Conservation Service (SCS), now Natural Resources Conservation Service (NRCS) developed a Dimensionless Unit Hydrograph (DUH) based on the analysis of large
number of watersheds. The X-axis consists of dimensionless time units and Y-axis consists of dimensionless discharge units. The DUH is very useful for constructing a synthetic unit
hydrograph for a wide variety of watersheds.
The SCS DUH consists of 37.5% of the total runoff volume before the peak discharge
and remaining volume after the peak discharge occurs. The total base of the DUH is
5 times the time to peak (Tp).
The DUH can be solved using simplified form of 'triangular' unit hydrograph. Assuming
same 37.5% of the volume on left of Tp for the triangular unit hydrograph,
we can solve for the Tb, which contains entire 100% volume of runoff.
Therefore, Tb = 1/0.375 = 2.67Tp.
From the figure above,
Converting the above equation so as to express the area under the unit hydrograph as 1 inch from the drainage area of 1 square mile in 1 hour, we get following equation:
As we know, the time base of the unit hydrograph is Tb = 2.67Tp
and Tb = Tp + Tr hence,
Tr = 1.67Tp
Substituting this value in the above equation, yields,
Where,
A is the drainage area in square miles
Q is the runoff volume in inches
Tp is the time to peak in hours, and
qp is the peak flow rate in cfs.
The peak rate factor of 484 has the inherent assumption that 3/8 of the volume under the unit hydrograph is under the rising limb and the remaining 5/8 of the volume is under the recession limb. This may not be true if the study area has characteristics requiring a lower or higher peak factor. The National Engineering Handbook by NRCS (March 2007) acknowledged several studies after 1972 depicted the variation in peak rate factors from below 100 to more than 600. Therefore, it is recommended that the Peak Rate Factor (PRF) should be modified depending upon the geographic conditions. In general, higher PRF should be used for steeper watersheds, and lower PRF should be used for watersheds with milder slopes (e.g. coastal watersheds).
To use the SCS DUH, we need to determine only two things:
1. Time to peak, Tp (hr), and
2. Peak discharge, qp (cfs).
The time to peak can be determined as follows:
Tp=(D/2)+Tl,
where,
Tl is the lag time (hr) and
D = duration of the rainfall (hr),
The DUH has point of inflection located at approximately 1.7Tp. So,
using our relation of Tl=0.6*Tc, we can compute D as:
D = 0.2*Tp or D = 0.133*Tc.
Small variation in D is ok, but it should not exceed 0.25Tp
or 0.17Tc.
The peak discharge can be determined as follows:
qp=(484*A)/Tp, which is same as the equation shown previously,
but with Q = 1.0 inch for the unit hydrograph.
If you need to determine the discharge for any other runoff volume, you can
multiply the qp with appropriate runoff depth, Q (in).
Once we determine Tp and qp, we can calculate D-hr unit hydrograph for our drainage area of interest using following co-ordinates:
After calculating D-hr unit hydrograph, you can calculate unit hydrograph for any other duration using previously discussed technique of S-hydrograph.
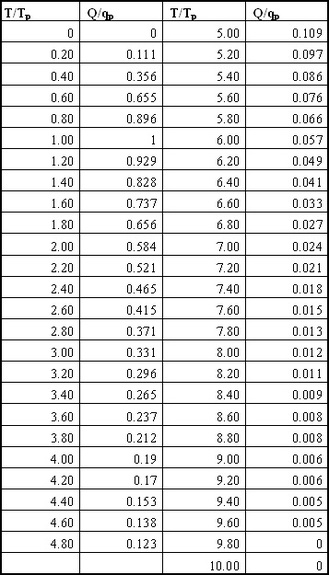
Delmarva Unit Hydrograph
If you have a watershed characterized by a flat terrain (for example, coastal
watershed), you may wish to use lower peak rate factor. NRCS has published the
Delmarva Unit Hydrograph particularly suited for the flat coastal areas in Delaware,
Maryland, Virginia and New Jersey.
If your drainage area of interest falls in this area, you may wish to use following
Delmarva unit hydrograph co-ordinates instead of SCS DUH.
Note that the volume of runoff prior to peak discharge is 22% vs. 37.5% for SCS DUH.
Also the base is 10Tp vs. 5Tp for SCS DUH.
Also, don't forget
to use the PRF of 284 instead of 484.