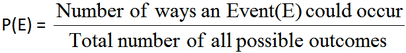Probability
Experiment: It is a process of observing a phenomenon that has an uncertain/variable outcomes.
Sample Space: It is the set of all possible distinct outcomes from an experiment. For example, the sample space for a couple having two childrens is: BB, BG, GB, GG. (B=boy, G=girl).
Event (E): It is a set of sample space outcomes for a desired feature. For example, the event that the couple will have one boy is: BB, BG, GB.
Probably of an event P(E): Sum of the probabilities of all outcomes for a given event.
Example:
What is the probability of getting a head on tossing a fair coin?
Answer: There are only two possible outcomes. We get either a head or a tail. Therefore, the probability of getting a head is 1/2.
Following defines the Probability of an Event - P(E)
Two important definition are necessary to understand here before we proceed with the Multiplication rule of probability.
Independent Events:
Two events are considered independent of each other if the outcome of one event does not depend on the outcome of other event.
Example: What is the probability of getting a tail in second toss during an experiment of tossing a fair coin twice ? Are these events independent or dependent ?
Answer:In this example the outcome of second toss does not depend on whether it was tail or head in the first toss.
These two events are considered independent of each other. In this example, the probability of getting a tail in second toss is 0.5 regardless
of what the outcome was in the first toss.
Dependent Events:
If the outcome of an event or experiment depends on the outcome of other event then the event is called a dependent event.
Example: Joe decides that he needs to give himself a break after studying Statistics for a week. He decides to go out tomorrow. The chances of raining tomorrow is 70%.
He will go to a Casino or a Movie if it rains tomorrow otherwise he'll go either surfing or golfing. However, he could not fall asleep and was wondering
what is the probability that it will rain tomorrow and he will go to the Casino? Your role is to be a Statistician who will give him his answer so that
he can fall asleep for an energetic day tomorrow.
(Assume that the probability of Joe choosing between Casino and Movie is equal).
Answer: Unlike the previous example of tossing a fair coin twice, here the events are dependent. To determine the probability of
Joe going to a Casino, we need to take into account the information regarding the chances of rain: P(R)=0.70. Here the probability of raining tomorrow and
Joe going to a Casino is P(RC)=P(R)*P(C/R)=0.70*0.50=0.35. See 'Multiplication Rule' for probability below. P(C/R) is read as Probability of C given that an
event R has already occured.
Multiplication Rule
Multiplication rule for independent events: The probability of two independent events A and B occurring together is:
P(AB)=P(A)*P(B).
Multiplication rule for dependent events: The probability of two dependent events A and B occurring together is:
P(AB)=P(A)*P(B/A)
It is necessary to introduce here the concept of exclusivity of an events to better understand the Addition rule of probability.
Mutually Exclusive Events: If the occurrence of an event guarantees that the other events cannot occur then the events are said
to be mutually exclusive events. For example, in an experiment of a roll of die, there is only one possible outcome. It could be either 1, 2, 3, 4, 5 or 6.
They cannot occurr together. They are mutually exclusive events. In simple terms, mutually exclusive events are those that cannot occur simultaneously.
Addition Rule
Addition rule for mutually exclusive events: The probability of occurrence of A or B is:
P(A or B)=P(A)+P(B).
Example: In a fruit basket containing 50 fruits, there are 10 apples(A) and 5 oranges(O). Remaining 35 are other fruits. You hate both apples and oranges.
If you pick one fruit (without looking or guessing by touch !!), What is the probability that you'll get your hated fruit (i.e.,either apple or an orange)?
Answer: Here the events are mutually exclusive. i.e., you can get one and only one type of fruit when you pick a fruit.
Therefore P(A or O)=P(A)+P(O)=(10/50)+(5/50)=0.30.
Addition rule for nonmutually exclusive events: The probability of occurrence of A or B is:
P(A or B)=P(A)+P(B)-P(A and B).
Example: In a movie theatre with 100 seats (fully occupied), there are 60 women(W) and 40 men(M).
Among the viewers, there are 45 women and 25 men who likes Julia Roberts(J). If you choose one seat at random, what is
the probability that the person is a women(W) or a viewer who likes Julia Roberts(JL)?
Answer: Here the events are not mutually exclusive. It is possible that the seat you choose has a person that is a women and likes Julia Roberts.
Therefore you cannot add both probabilities directly. You have to discount the probability of 'overlap'.
Therefore P(W or JL)=(P(W)+P(JL)-P(W and JL)=(60/100)+(70/100)-(45/100) = 0.85.
Notice that the P(JL)=(45+25)/100=(70/100) in the above equation.