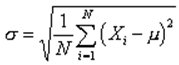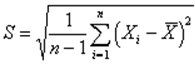Dispersion

Range It is the difference between highest and lowest value in the data set. Range provides some idea about the variability in the data (more than the mean alone). The range could be misleading if one of the extreme value is atypical.

Interquartile Range (IQR) It is the better measure of dispersion than the Range. It uses the terms Q₁, Q₂, Q₃, Q₄ to denote each quarter of the data set. Q₁ lies at the 25th percentile, Q₂ lies at the 50th percentile or median, Q₃ lies at the 75th percentile, and Q₄ lies at the 100th percentile. The IQR is obtained by Q₃ - Q₁.i.e., the value at the 75th percentile minus the value at the 25th percentile.

Standard Deviation (s) It is the better measure of dispersion compared to range and IQR because unlike range and IQR, the Standard deviation utilizes all the values in the data set in its calculation. The square of the standard deviation is called Variance(s²). Following is formula for computing standard deviation for population or sample data. The differnce between two values becomes small as 'n' becomes large. It is necessary to substract 1 from 'n' because it provides the correction for the bias, i.e., the sample has less variation or standard deviation than the population.

Standard Deviation for Population

Standard Deviation for Sample

Example: Calculate the standard deviation for Joe's income. Use the table provided under the section for 'Mean'.
Answer:10250 (using formula for population)
If we were to calculate standard deviation using formula for sample standard deviation, the answer would be 10668.

Coefficient of Variation (CV) Another important mean of measuring variation is 'Coefficient of Variation', commonly written as CV. It is useful when we want to compare variation between two different distributions. When the units of variable in two distributions is different, CV provides better means to compare them.
CV=(s*100)/x̄
For example, if you want to compare the variation in the income level between two countries, CV is a better measure than Range, IQR or standard deviation because the unit of variable (here currency) is different.

Skewness Skewness is used to measure excessive weight on either side of the center.
Skewness is measured as:
α = ¹/_n ∑(x_i - µ)³
The unbiased estimate of skewness for sample is:
a= ⁿ/_(n-1)(n-2)∑(x_i - x̂)³
The normal curve has no skewness (i.e., zero). The curve skewed to the right (i.e., long tail on right side) has positive skew and the curve skewed to the left (i.e., long tail on left) has negative skew value.

Continue to Next Topic (Probability)-Click Here