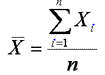Central Tendency
Central tendency involves finding out the central value about which the data is distributed. We mainly use one of the three measures for estimating the central tendency: Mean, Median and Mode.
Mean
It is the value obtained by dividing the sum of the measurements by total number of measurements added.
Mean
It is the value obtained by dividing the sum of the measurements by total number of measurements added.
Example: Estimate Joe's Mean Annual Income from 13 year data
| 2000 | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 40,000 | 45,000 | 49,000 | 56,000 | 52,000 | 51,000 | 58,000 | 62,000 | 29,000 | 35,000 | 50,000 | 60,000 | 65,000 |
Answer: 50,154
Median
It is the value in the middle of the sorted data. If the number of observations is odd, then median is the exact middle value of the sorted data, i.e., the value of {(n+1)/2}th observation. If the number of observations is even, then the median is the average value of two middle observations i.e., (n/2) and {(n+1)/2}th observations.
Example:Find the median for the Joe's Annual Income data provided above. Answer: 51,000 (Hint: First arrange the values in ascending order. Then find the middle value).
Mode
It is the most frequently occurring value in the observations.
Example:Find the mode for the following set of data.
| Observation No. | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| Value | 4 | 6 | 9 | 4 | 9 | 6 | 6 |