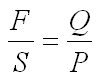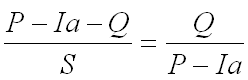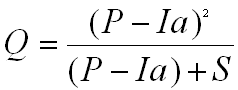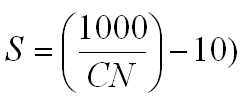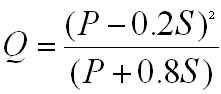SCS Runoff Curve Number Method
The conceptual basis of the curve number method has been the object of both support and criticism (Ponce and Hawkins, 1996). The major disadvantages of the method are sensitivity of the method to Curve Number (CN) values, fixing the initial abstraction ratio, and lack of clear guidance on how to vary Antecedent Moisture Conditions (AMC). However, the method is used widely and is accepted in numerous hydrologic studies. The SCS method originally was developed for agricultural watersheds in the mid-western United States; however it has been used throughout the world far beyond its original developers would have imagined.
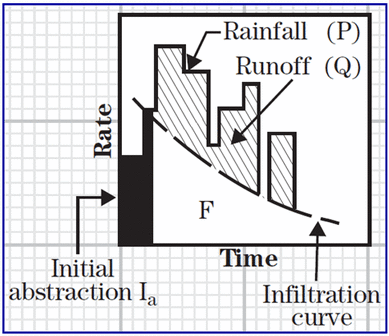
The basis of the curve number method is the empirical relationship between the retention (rainfall not converted into runoff) and runoff properties of the watershed and the rainfall. Mockus found equation 1 appropriate to describe the curves of the field measured runoff and rainfall values (National Engineering Handbook, 2004). Equation 1 describes the conditions in which no initial abstraction occurs.
Q = actual runoff
S = potential maximum retention after runoff begins (S ³ F)
P = potential maximum runoff (i.e., total rainfall if no initial abstraction).
For most applications, a certain amount of rainfall is abstracted. The three important abstractions for any single storm event are rainfall interception (Meteorological rainfall minus throughfall, stem flow and water drip), depression storage (topographic undulations), and infiltration into the soil. The curve number method lumps all three abstractions into one term, the Initial abstraction (Ia), and subtracts this calculated value from the rainfall total volume. The total rainfall must exceed this initial abstraction before any runoff is generated. This gives the potential maximum runoff (rainfall available for runoff) as P – Ia. Substituting this value in equation 1 yields following equation:
Ia = 0.2S Equation 4
The potential maximum retention S is related to the dimensionless parameter CN in the range of 0 <= CN <= 100 by Equation 5.
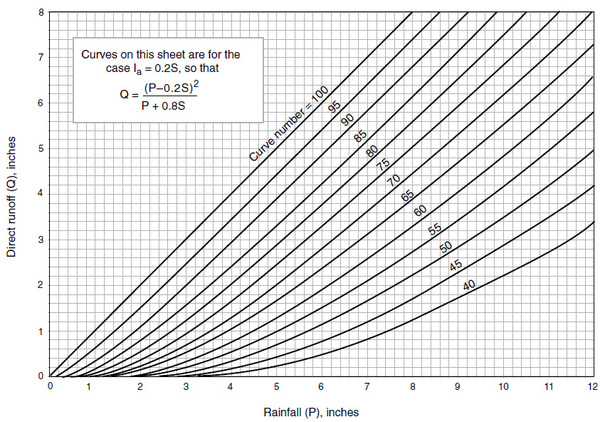
The solution of the SCS runoff equation is shown below:
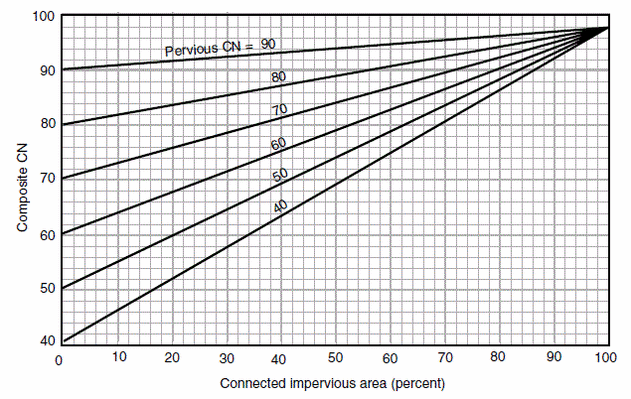
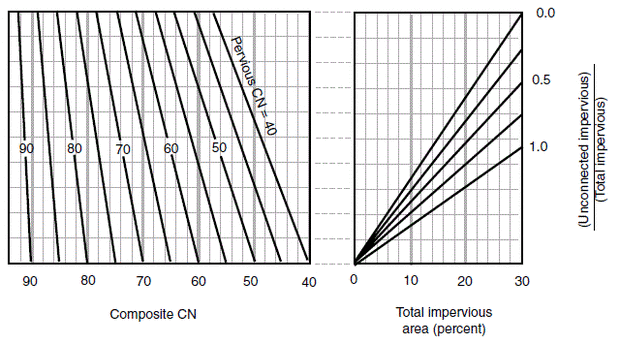
When the drainage area consists of landuse with impervious cover (Directly Connected or Unconnected), TR 55 provides separate graphs for computing the composite curve number values depending on the percent of the impervious cover. However, it is a good practice to calculate the runoff from impervious area and pervious area separately and then add the volume.
Example:Calculate the runoff depth for the 100 year storm event
over the watershed with an average CN of 75 using the SCS Runoff Method. The
design rainfall for 100 year storm event is 8.5 inches and drainage area is approximately 120 acres.
Solution: Follow the steps below:
Using equation 5 above, calculate the maximum potential retention S.
Using equation 6 above, calculate the runoff depth.
Multiply the Q inches with the drainage area and convert the units to commonly used volume units of 'ac-ft'.
Feel free to download TR-55 using the link provided below. It is in the public domain and therefore no copyright applies to it. Enjoy your reading and also feel free to post your questions/comments, which will be helpful to other users.
| tr55.pdf | |
| File Size: | 1986 kb |
| File Type: | |